Runners up in New Zealand Engineering Science Competition
Posted on November 03, 2020
Macleans College entered 18 teams in the 2020 New Zealand Engineering Science Competition.
The following team of Year 13 students were overall runners up in the event. They were Darsh Chaudhari (Batten House), Daniel Ahn (Batten), Yunge Yu (Hillary) and Jimmy Zhou (Batten). Their achievement was impressive as 1038 individual students participated in 268 teams from 82 schools around New Zealand. They received a prize of $2000.
This annual problem-solving competition was held from 10 am – 6 pm. The students worked on the following question; how many satellites can be launched into orbit before astronomers on earth can no longer observe the night sky without interruption?
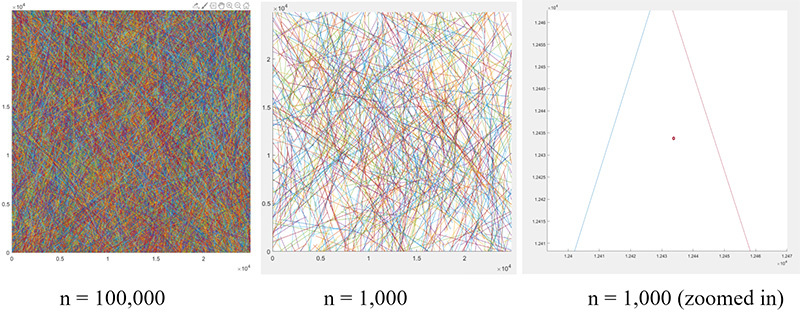
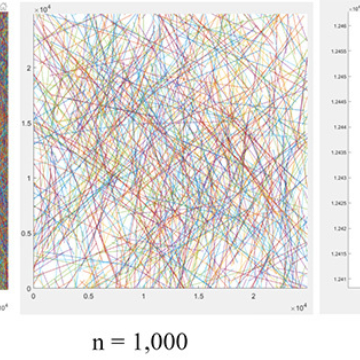
The team chose to simulate the movement of satellites across the night sky over a time equivalent to the exposure time of an average f/7 telescope taking into account orbital velocity and the earth's rotation. Finally, they graphed the mean number of interruptions against the number of satellites (n) to get an answer of 106,690 satellites at a height of lower earth orbit.
Macleans College entered 18 teams in the 2020 New Zealand Engineering Science Competition.
The following team of Year 13 students were overall runners up in the event. They were Darsh Chaudhari (Batten House), Daniel Ahn (Batten), Yunge Yu (Hillary) and Jimmy Zhou (Batten). Their achievement was impressive as 1038 individual students participated in 268 teams from 82 schools around New Zealand. They received a prize of $2000.
This annual problem-solving competition was held from 10 am – 6 pm. The students worked on the following question; how many satellites can be launched into orbit before astronomers on earth can no longer observe the night sky without interruption?
The team chose to simulate the movement of satellites across the night sky over a time equivalent to the exposure time of an average f/7 telescope taking into account orbital velocity and the earth's rotation. Finally, they graphed the mean number of interruptions against the number of satellites (n) to get an answer of 106,690 satellites at a height of lower earth orbit.